Introdução
As redes neurais profundas revolucionaram diversas áreas da tecnologia, desde o reconhecimento de imagens até o processamento de linguagem natural. Neste artigo, exploraremos os fundamentos matemáticos que sustentam essas poderosas ferramentas de aprendizado de máquina.
O Neurônio Artificial
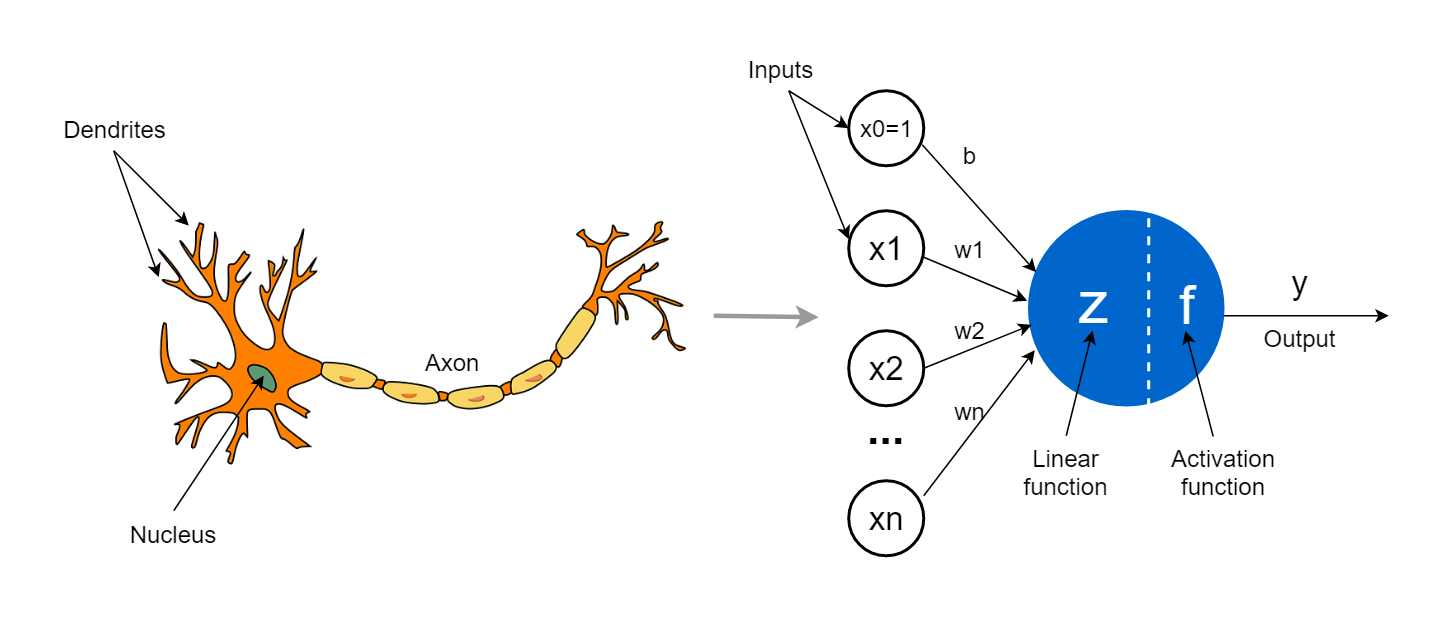
O neurônio artificial é a unidade básica de uma rede neural. Matematicamente, podemos representá-lo como uma função que recebe múltiplas entradas, aplica pesos a essas entradas, soma os resultados e passa essa soma por uma função de ativação.
Onde:
1. X_i são as entradas
2. w_i são os pesos associados a cada entrada
3. b é o termo de viés (bias)
4. f é a função de ativação
5. y é a saída do neurônio
Funções de Ativação
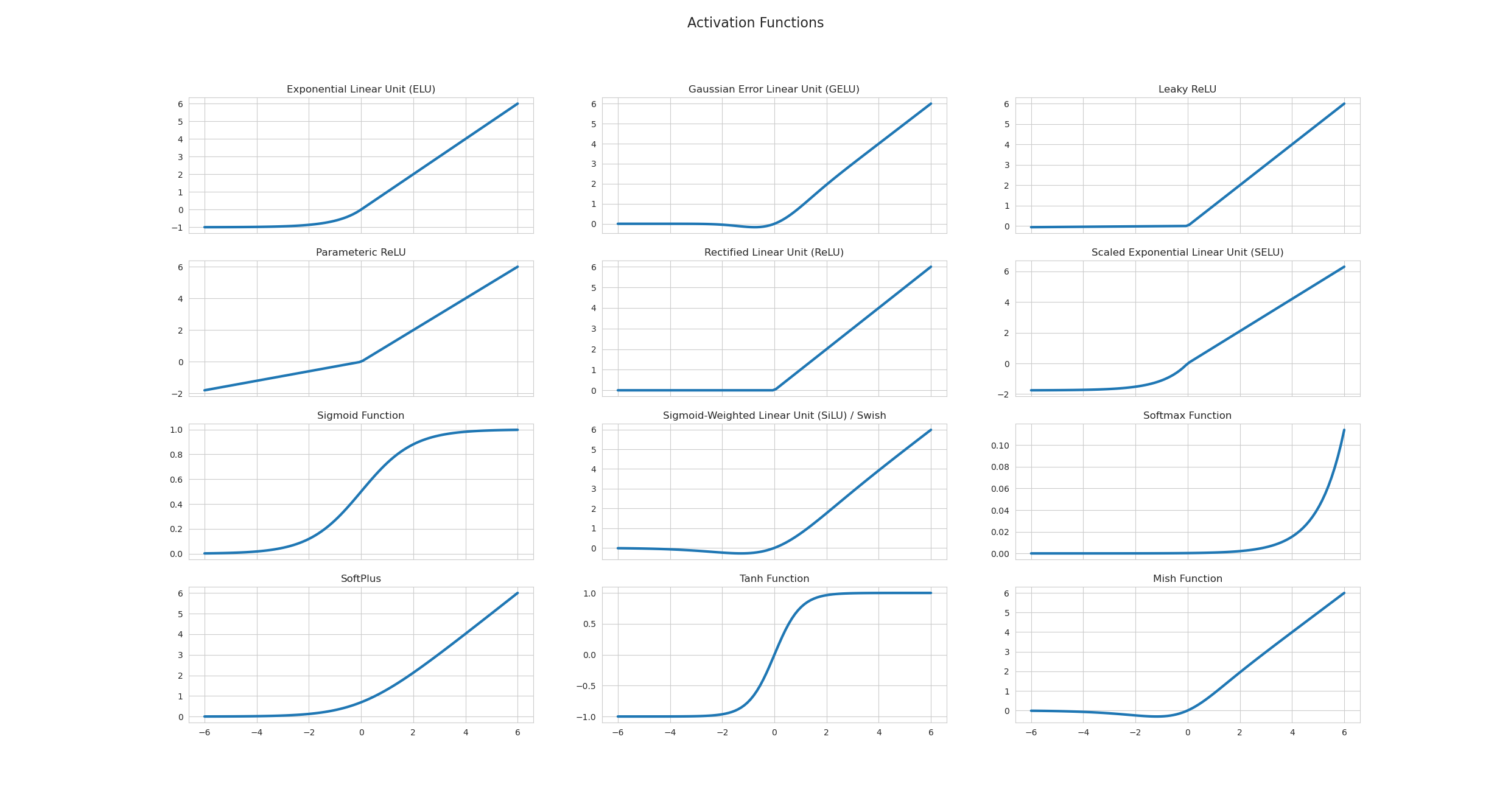
As funções de ativação introduzem não-linearidades no modelo, permitindo que a rede neural aprenda padrões complexos. Algumas das funções de ativação mais comuns incluem:
Sigmoid
A função sigmoid comprime a saída para o intervalo $(0,1)$, sendo útil para problemas que envolvem probabilidades.
ReLU (Rectified Linear Unit)
A ReLU é computacionalmente eficiente e ajuda a mitigar o problema do desaparecimento do gradiente.
Tangente Hiperbólica
A tangente hiperbólica produz saídas no intervalo $(-1,1)$ e possui propriedades semelhantes à sigmoid.
Arquitetura de Redes Neurais Profundas
Uma rede neural profunda consiste em múltiplas camadas de neurônios conectados entre si. Temos:
1. Camada de entrada: Recebe os dados iniciais
2. Camadas ocultas: Realizam transformações nos dados
3. Camada de saída: Produz o resultado final
Matematicamente, a propagação direta (forward propagation) através de uma rede neural com $L$ camadas pode ser expressa como:
Onde:
1. a^{[l]} é a ativação da camada
2. W^{[l]} é a matriz de pesos da camada
3. b^{[l]} é o vetor de viés da camada
g^{[l]} é a função de ativação da camada
\hat{y} é a previsão final da rede
O treinamento de redes neurais ocorre através do algoritmo de retropropagação (backpropagation), que calcula os gradientes para atualizar os pesos e vieses da rede. O processo inicia calculando o erro entre a saída prevista $\hat{y}$ e o valor real $y$:
Onde $L$ é uma função de perda apropriada, como a entropia cruzada para classificação ou erro quadrático médio para regressão. O algoritmo de backpropagation usa a regra da cadeia para calcular os gradientes:
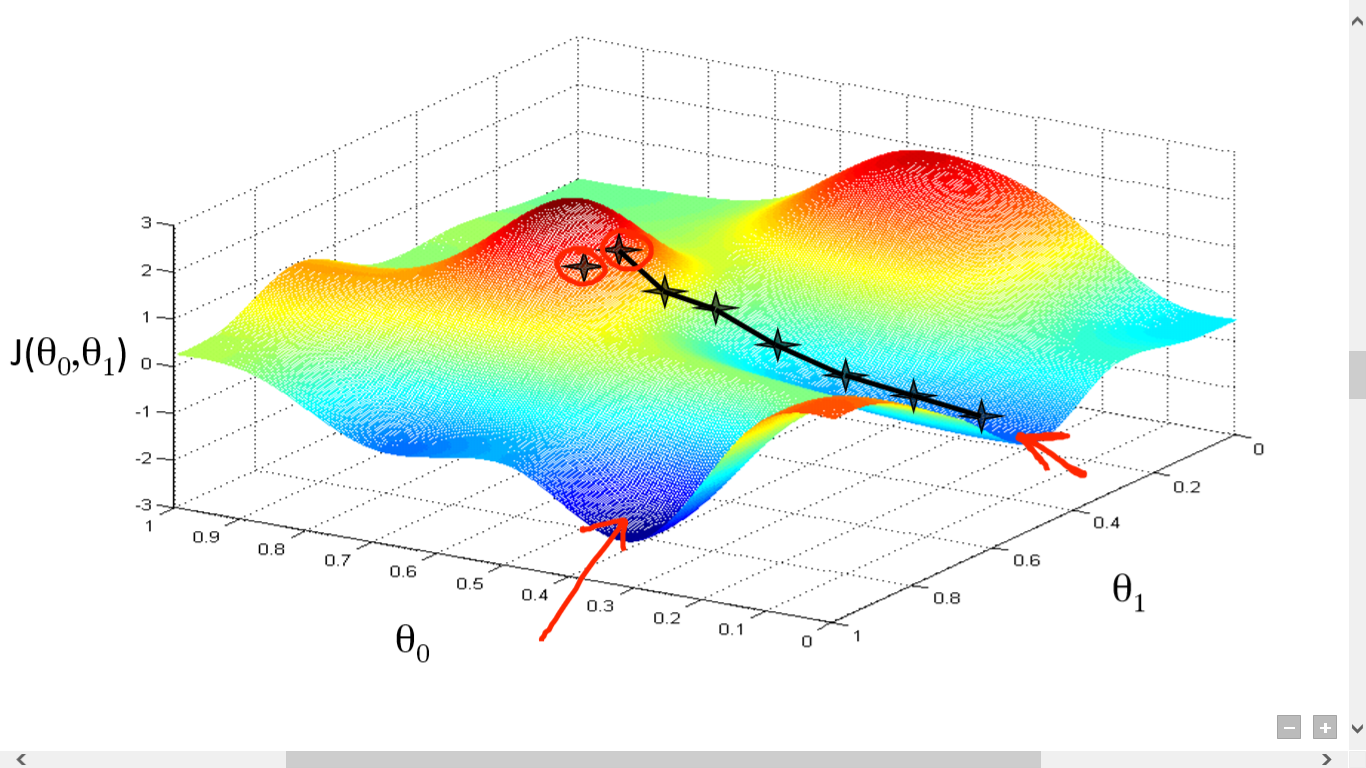
Os pesos e vieses são então atualizados usando um algoritmo de otimização, como o Gradiente Descendente:
Onde $\alpha$ é a taxa de aprendizado.
Regularização
Para evitar o overfitting, técnicas de regularização são aplicadas. A regularização L2, por exemplo, adiciona um termo à função de custo:
Onde $\lambda$ é o parâmetro de regularização e $||W||^2_F$ é a norma de Frobenius da matriz de pesos. Outras técnicas incluem Dropout, onde neurônios são aleatoriamente desativados durante o treinamento:
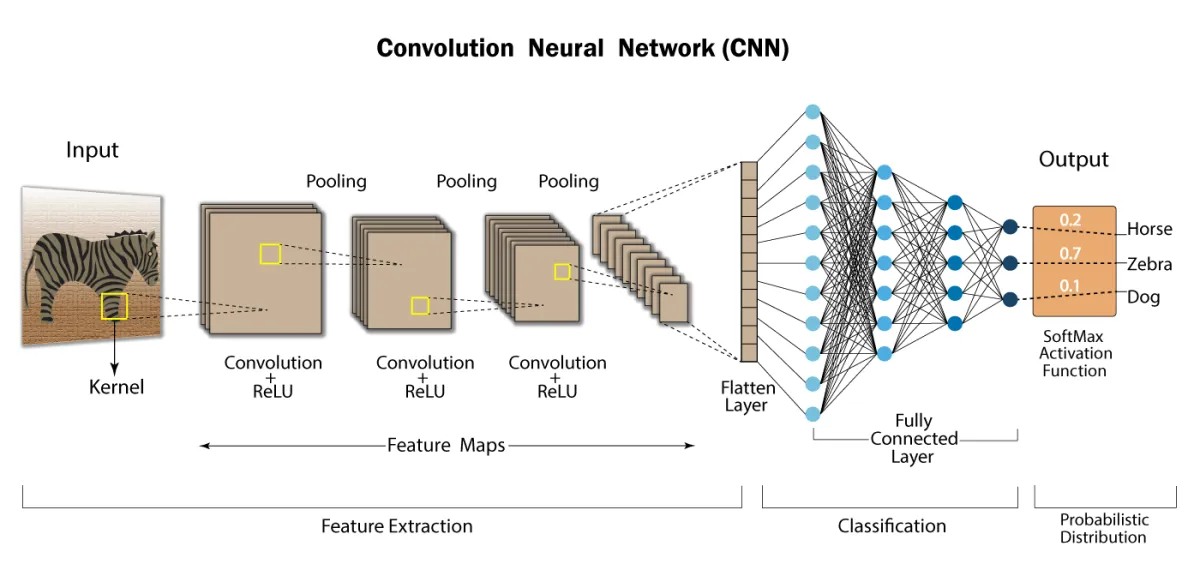
Redes Neurais Convolucionais (CNNs)
As CNNs são especialmente eficazes para processamento de imagens. A operação de convolução é definida como:
Em redes neurais, a convolução discreta 2D é utilizada:
Onde $I$ é a imagem de entrada e $K$ é o kernel.
Redes Neurais Recorrentes (RNNs)
As RNNs são projetadas para processar sequências temporais, mantendo um estado interno:
Onde:
1. $h_t$ é o estado oculto no tempo $t$
2. $x_t$ é a entrada no tempo $t$
3. $y_t$ é a saída no tempo $t$
4. $W_{hx}$, $W_{hh}$, $W_{yh}$ são matrizes de peso
5. $b_h$, $b_y$ são vetores de viés
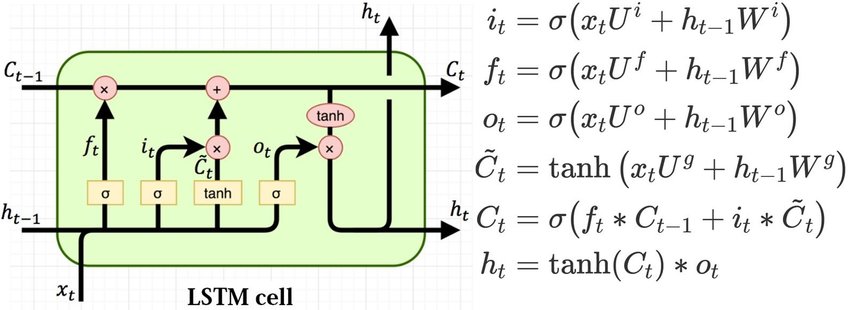
LSTMs e GRUs
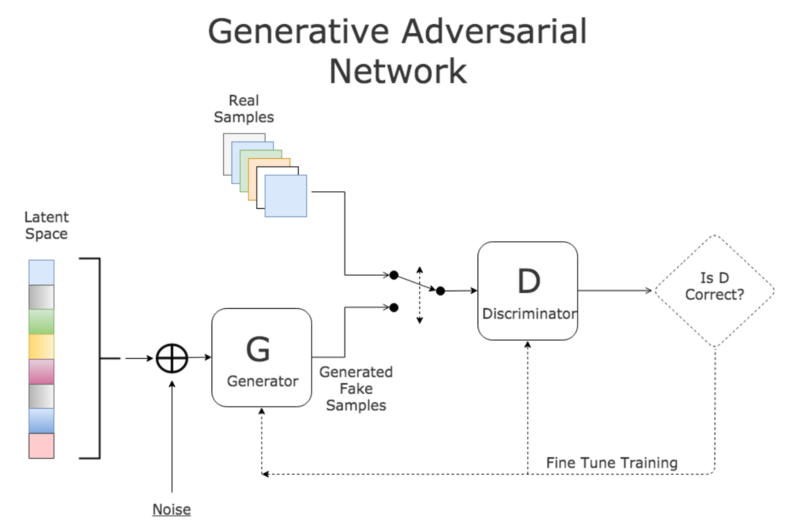
Redes Generativas Adversariais (GANs)
As GANs consistem em dois componentes: um gerador $G$ e um discriminador $D$. O jogo minimax entre $G$ e $D$ é definido como:
Onde:
1. $p_{data}$ é a distribuição dos dados reais
2. $p_z$ é a distribuição do ruído de entrada
3. $G(z)$ é o gerador que mapeia o ruído para dados sintéticos
4. $D(x)$ é o discriminador que estima a probabilidade de $x$ ser real
Conclusão
As redes neurais profundas são estruturas matemáticas complexas que permitem a modelagem de padrões intrincados nos dados. Embora tenhamos abordado apenas os fundamentos, espero que esta introdução matemática ajude a elucidar os princípios por trás dessas poderosas ferramentas de aprendizado de máquina.
Referências
Goodfellow, I., Bengio, Y., Courville, A. (2016). Deep Learning. MIT Press.
LeCun, Y., Bengio, Y., Hinton, G. (2015). Deep learning. Nature, 521(7553), 436-444.
Rumelhart, D. E., Hinton, G. E., Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
